Articolo redatto per 

Dal modello di Markowitz all’ottimizzazione EasySampling: strumenti evoluti per la consulenza finanziaria moderna

La correlazione è come una danza silenziosa tra asset: alcuni si muovono all’unisono, altri si respingono, altri ancora sembrano ignorarsi a vicenda. Ma cosa accade quando questa danza cambia ritmo, in un mondo finanziario in cui l’imprevisto è la sola costante? In questo scenario, affidarsi a una fotografia statica del passato non basta più. Serve un modello dinamico, un occhio più consapevole: occorre robustezza.

La matrice di correlazione: fondamento teorico e limiti strutturali

La matrice di correlazione è una delle pietre miliari nella teoria del portafoglio. Essa codifica, con rigore matematico, le interrelazioni lineari tra i rendimenti degli strumenti finanziari. In una matrice quadrata e semi-definita positiva[1], ogni elemento rappresenta un coefficiente di correlazione di Pearson tra due asset, misurando la loro sincronia o disaccordo nei movimenti di prezzo.

Nel contesto della Modern Portfolio Theory, la matrice diventa lo strumento principe per minimizzare la varianza complessiva di portafoglio, consentendo di costruire la cosiddetta frontiera efficiente. Tuttavia, questa eleganza teorica s’infrange spesso con l’instabilità dei mercati reali. La crisi finanziaria del 2008, il crollo dei titoli tecnologici nel 2000, o ancora la pandemia da COVID-19 hanno mostrato come correlazioni storiche possano sgretolarsi in tempi brevissimi, lasciando i portafogli esposti a rischi sistemici non previsti dal modello teorico.

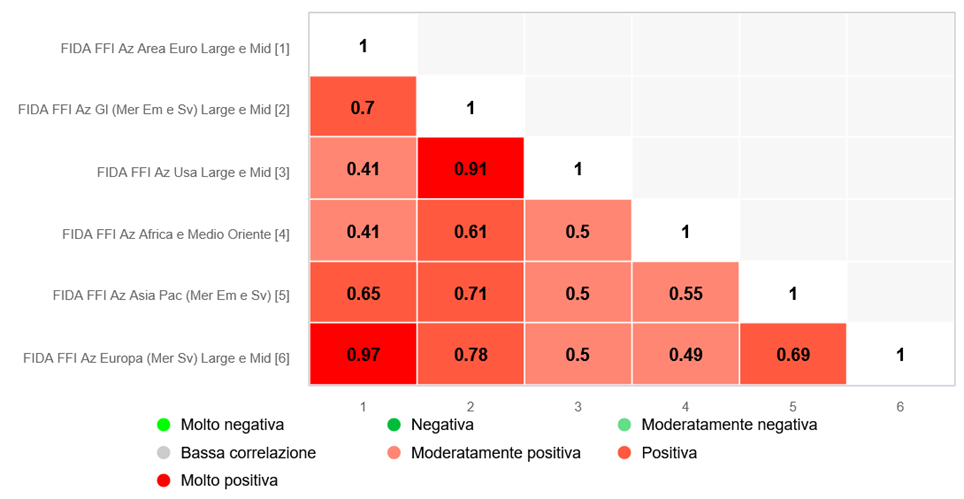
Fonte: FIDAworkstation

L’illusione della stabilità

I modelli classici assumono che correlazioni e varianze siano stabili nel tempo e perfettamente stimabili. Ma la realtà è ben diversa: shock macroeconomici, eventi esogeni e transizioni di regime[2] rendono le correlazioni altamente instabili. Le stime puntuali rischiano dunque di produrre portafogli otticamente ottimali ma praticamente disfunzionali, con sovra-concentrazioni e performance incoerenti.

Questo problema si aggrava all’aumentare della dimensionalità del portafoglio: più titoli si includono, più la matrice di correlazione diventa difficile da stimare correttamente, con il rischio di introdurre rumore più che informazione. Inoltre, il comportamento aggregato degli investitori può causare la cosiddetta “correlazione da panico”, in cui asset tradizionalmente decorrelati si muovono all’unisono nei momenti di crisi, vanificando l’illusione della diversificazione.

Il paradigma della robustezza: oltre la fotografia, verso il film

’ottimizzazione robusta nasce per rispondere a questa criticità. Invece di fondarsi su un’unica matrice di correlazione, considera l’incertezza insita nei parametri. Il risultato è un portafoglio meno sensibile a errori di stima e più stabile al variare degli scenari.

Alcuni approcci robusti introducono intervalli di confidenza sui parametri stimati, assumendo che questi non siano fissi ma distribuiti entro un range di plausibilità statistica. In quest’ottica, il portafoglio ottimale non è più quello che massimizza il rendimento atteso su un solo scenario, ma quello che mantiene le sue proprietà su una famiglia di scenari alternativi.

I metodi bayesiani, da parte loro, integrano le stime puntuali con informazioni a priori: anziché trattare i parametri come valori certi, li considerano come variabili casuali dotate di distribuzioni di probabilità. Questo consente di incorporare conoscenza esperta, dati esterni o intuizioni di mercato, rendendo l’allocazione finale un compromesso tra evidenza storica e giudizio analitico.

Le simulazioni bootstrap, infine, costituiscono una tecnica non parametrica estremamente efficace per testare la resilienza dei portafogli. Attraverso il ri-campionamento con reinserimento di osservazioni storiche, generano una moltitudine di scenari alternativi che conservano le caratteristiche statistiche di partenza, ma esplorano l’intero spettro delle possibili evoluzioni. Il portafoglio che si dimostra solido attraverso molteplici simulazioni ha maggiori probabilità di performare con coerenza anche nel mondo reale.

Il concetto di robustezza non è sinonimo di conservatorismo, bensì di consapevolezza dell’imperfezione dei dati. Costruire un portafoglio robusto significa abbracciare l’incertezza, non eluderla; significa progettare per la variabilità, anziché sperare nella stabilità.

EasySampling con FIDAworkstation

È in questo contesto che si colloca EasySampling, il modulo di ottimizzazione media-varianza integrato nella piattaforma FIDAworkstation. Il metodo consiste nel campionare l’orizzonte storico in dieci sottoperiodi annuali, rappresentativi di scenari differenti. Per ciascun campione si calcolano correlazioni, varianze e rendimenti, costruendo dieci diverse frontiere efficienti.

La metodologia si rifà idealmente al bootstrap statistico: suddividendo l’arco temporale in sotto-periodi indipendenti, si ottiene una visione policroma dell’universo investibile, che riflette una molteplicità di condizioni di mercato, dai regimi bull a quelli recessivi.

L’utilizzo della base dati FIDA FFI (FIDA Fund Index) garantisce un’ampia copertura cross-asset, fondata su dati di qualità certificata. La scelta di campioni annuali su un orizzonte decennale consente di cogliere variazioni cicliche e di stressare il portafoglio rispetto a condizioni eterogenee.

Il risultato finale è una asset allocation media: più robusta, meno condizionata da eventi anomali, capace di riflettere la natura dinamica e imperfetta dei mercati. L’output è pienamente integrabile nel flusso operativo del consulente finanziario, anche grazie alle funzionalità grafiche e comparative offerte dalla piattaforma.

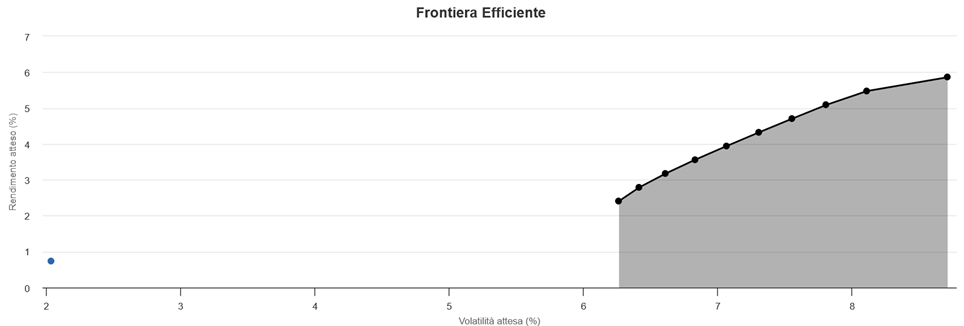
Fonte: FIDAworkstation

Un approccio più umano alla gestione: l’antifragilità applicata ai portafogli

Lungi dall’essere un vezzo tecnico, la robustezza è un modo diverso di concepire la consulenza: non più come arte della previsione, ma come architettura della resilienza. EasySampling consente al professionista di costruire portafogli che non solo resistono al cambiamento, ma ne traggono beneficio.

Il richiamo al concetto talebiano di “antifragilità” non è casuale: un portafoglio costruito su asset allocation mediate da diversi regimi storici tende a non collassare in presenza di stress, ma anzi a sfruttare le inefficienze momentanee del mercato. Non si tratta quindi solo di difendere il capitale, ma di prosperare nel disordine.

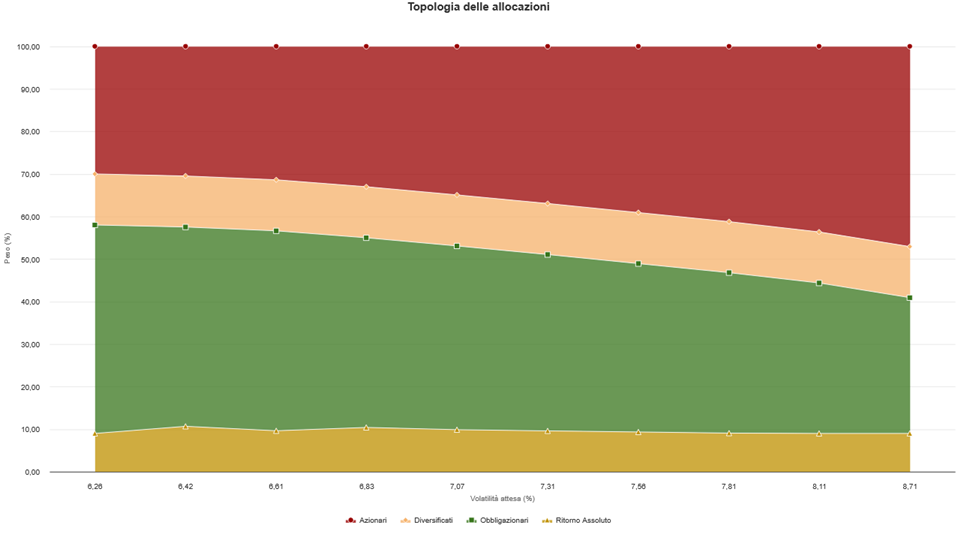
Fonte: FIDAworkstation

La consulenza come ingegneria dell’incertezza

Nel passaggio dalla teoria alla pratica, la matrice di correlazione perde la sua veste di strumento perfetto per diventare un oggetto critico, da maneggiare con consapevolezza. Moduli avanzati come EasySampling rappresentano l’evoluzione naturale di un approccio ormai maturo: quello che sa che l’incertezza è inevitabile, ma non ingestibile.

Affiancare la teoria del portafoglio con strumenti computazionali sofisticati ma intuitivi non significa tradirne l’eleganza matematica, bensì tradurla in efficienza operativa. In questo senso, FIDAworkstation si propone come alleato prezioso del consulente contemporaneo: non come oracolo, ma come officina razionale in cui l’analisi quantitativa si fa mestiere quotidiano

Riferimenti:

• Markowitz, H. (1952). Portfolio Selection. Journal of Finance
• Efron, B. (1979). Bootstrap Methods: Another Look at the Jackknife. Annals of Statistics
• Ben-Tal, A., & Nemirovski, A. (2002). Robust Optimization – Methodology and Applications. Mathematical Programming
• Meucci, A. (2005). Risk and Asset Allocation. Springer
• Elton, E. J., Gruber, M. J., Brown, S. J., & Goetzmann, W. N. (2014). Modern Portfolio Theory and Investment Analysis. Wiley
• Taleb, N. N. (2012). Antifragile: Things That Gain from Disorder. Random House

[1] L’espressione “semi-definita positiva” è un concetto matematico che descrive una proprietà fondamentale delle matrici di covarianza e di correlazione. In termini semplici, significa che per qualsiasi vettore non nullo χ, il prodotto χ^⊤Aχ (dove A è la matrice in questione) è maggiore o uguale a zero.

Nel contesto della matrice di correlazione, questa proprietà garantisce che non esistano combinazioni lineari di asset che producano una varianza negativa (che sarebbe assurda, visto che la varianza è una misura di dispersione e dev’essere sempre positiva o nulla). È una condizione necessaria perché il modello di Markowitz e le sue derivate siano matematicamente coerenti.

[2] L’espressione “transizioni di regime”, che in ambito finanziario indica il passaggio da un contesto di mercato a un altro caratterizzato da condizioni strutturali differenti. Ad esempio, un cambiamento repentino da uno scenario di tassi d’interesse bassi e liquidità abbondante a uno con inflazione persistente e politiche monetarie restrittive rappresenta una transizione di regime.

Monica F. Zerbinati

Richiedi la prova gratuita a welcometeam@fidaonline.com

Articolo completo su www.we-wealth.com